SOFUS ..
Functions
FNM Calculation functions
Fast Near-field Method
Collaboration diagram for FNM Calculation functions:

Functions

template<class T >
std::complex< T > CalcHz (const T &s, const T &l, const T &z, const T &k, const GLQuad2D< T > *gl)
 
template<class T >
int CalcCwFieldRef (const sysparm_t< T > *sysparm, const ApertureData< T > *data, const T *pos, const size_t nPositions, std::complex< T > **odata, void *pBar)
 
template<class T >
int CalcCwFieldFourRef (const sysparm_t< T > *sysparm, const ApertureData< T > *data, const T *pos, const size_t nPositions, std::complex< T > **odata)
 
template<class T >
int CalcCwFocusNaiveFast (const sysparm_t< T > *sysparm, const ApertureData< T > &data, const T *pos, const size_t nPositions, std::complex< T > **odata)
 
template<class T >
std::complex< T > CalcSingleFast (const T &s1, const T &s2, const T &l, const T &z, const T &k, const T *uxs, const T *uweights, const size_t nUs)
 
template<class T >
int CalcCwTimeReversal (const fnm::sysparm_t< T > *sysparm, const ApertureData< T > *pData0, const ApertureData< T > *pData1, const T *pos, const size_t nPositions, const std::complex< T > *pFieldValues, const size_t nComplexValues, std::complex< T > **odata, sps::ProgressBarInterface *pBar)
 
template<class T >
int CalcCwBackThreaded (const fnm::sysparm_t< T > *sysparm, const ApertureData< T > *data, const T *pos, const size_t nPositions, const std::complex< T > *pWeights, const size_t nWeights, std::complex< T > **odata, sps::ProgressBarInterface *pbar)
 
template<class T >
int CalcCwThreaded (const fnm::sysparm_t< T > *sysparm, const ApertureData< T > *data, const T *pos, const size_t nPositions, std::complex< T > **odata, sps::ProgressBarInterface *pbar)
 
template<class T >
void CalcCwField (const sysparm_t< T > *sysparm, const ApertureData< T > &data, const T *pos, const size_t nPositions, std::complex< T > **odata)
 
template<class T >
int CalcCwFocus (const sysparm_t< T > *sysparm, const ApertureData< T > &data, const T *pos, const size_t nPositions, std::complex< T > **odata)
 
template<class T >
int CalcCwFocusRef (const sysparm_t< T > *sysparm, const ApertureData< T > &data, const T *pos, const size_t nPositions, std::complex< T > **odata)
 

Detailed Description

Function Documentation

◆ CalcCwBackThreaded()

int CalcCwBackThreaded ( const fnm::sysparm_t< T > *  sysparm,
const ApertureData< T > *  data,
const T *  pos,
const size_t  nPositions,
const std::complex< T > *  pWeights,
const size_t  nWeights,
std::complex< T > **  odata,
sps::ProgressBarInterface *  pbar 
)

◆ CalcCwField()

void CalcCwField ( const sysparm_t< T > *  sysparm,
const ApertureData< T > &  data,
const T *  pos,
const size_t  nPositions,
std::complex< T > **  odata 
)

Naive integral, no re-use of parts and many abcissa are needed when projection is far away from rectangle.

Consider renaming to CalcCwNaive

Parameters
sysparm
data
pos
nPositions
odata

◆ CalcCwFieldFourRef()

int CalcCwFieldFourRef ( const sysparm_t< T > *  sysparm,
const ApertureData< T > *  data,
const T *  pos,
const size_t  nPositions,
std::complex< T > **  odata 
)

CalcCwFieldFourRef

Same as CalcCwFieldRef except the number of integrals is reduced to four

Parameters
sysparm
data
pos
nPositions
odata
Returns

◆ CalcCwFieldRef()

int CalcCwFieldRef ( const sysparm_t< T > *  sysparm,
const ApertureData< T > *  data,
const T *  pos,
const size_t  nPositions,
std::complex< T > **  odata,
void *  pBar 
)

Spatial impulse response computed at the positions pos for a frequency f0. The principle of superposition is used as shown below and the ranges of integration are reduced to give the most accurate result with the least amount of abcissas. This is a reference implementation. Eight integrals are evaluated, which can be reduced to four. See CalcCwFieldFourRef

The frequency f0 as well as the positional information for the aperture is contained in the ApertureData structure data.

Superposition principle: 

            ^
            |
      +-----+-----+-----------+ (x,y)
      |     |     |           |
      +-----+-----+-----------+
      |     |     |           |
      |     |     |           |
      |     |     |           |        =
      +     o-----+-----------+---->
      |           |           |
  hh  |           |           |
      |           |           |
      +-----+-----+-----------+
              hw

            ^                             ^                                     ^                                      ^
            |                             |                                     |                                      |
      +-----------------------+ (x,y)     |     +-----------+ (x,y)       +-----+-----+-----------+ (x,y)              |     +-----------+ (x,y)
      |     |                 |           |     |           |             |     |                 |                    |     |           |
      +     |                 |           |     |           |             +-----+-----------------+              +     |     +-----------+
      |     |                 |           |     |           |             |     |                                |     |
      |     |                 |           |     |           |         hh  |     |                            hh  |     |
      |     |                 |       -   |     |           |       -     |     |                        +       |     |
      |     o-----------------|---->      o-----+-----------+---->        +     o---------------------->         +     o---------------------->
      |                       |                 |           |                                                    |
  hh  |                       |                 |           |                                                    |
      |                       |                 |           |                                                    |
      +-----------+-----------+                 +-----------+                                                    +-----+-----+
              hw                            hw                                                                           hw

\begin{eqnarray} H(x,y,z,k) &= H_{hw+|x|,hh+|y|}(z;k) - H_{|x|-hw,hh+|y|}(z;k) - H_{hw+|x|,|y|-hh}(z;k) + H_{|x|-hw,|y|-hh}(z;k)\nonumber\\ &= H_{hw+|x|,hh+|y|}(z;k) + H_{hw-|x|,hh+|y|}(z;k) + H_{hw+|x|,hh-|y|}(z;k) + H_{hw-|x|,hh-|y|}(z;k)\nonumber\\ &= -\frac{i}{2\pi k} \Big( (hh+|y|)\int_{0}^{|x|+hw} M(hh+|y|,\sigma, z, k)d\sigma +(hw+|x|)\int_{0}^{|y|+hh} M(hw+|x|,\sigma, z, k)d\sigma \nonumber\\ &\phantom{= -\frac{i}{2\pi k} \Big(} -(hh+|y|)\int_{0}^{|x|-hw} M(hh+|y|,\sigma, z, k)d\sigma - (hw-|x|)\int_{0}^{|y|-hh} M(hw-|x|,\sigma, z, k)d\sigma\nonumber\\ &\phantom{= -\frac{i}{2\pi k} \Big(} - (hh-|y|)\int_{0}^{|x|-hw} M(hh-|y|,\sigma, z, k)d\sigma -(hw+|x|)\int_{0}^{|y|-hh} M(hw+|x|,\sigma, z, k)d\sigma \nonumber\\ &\phantom{= -\frac{i}{2\pi k} \Big(} + (hh-|y|)\int_{0}^{|x|+hw} M(hh-|y|,\sigma, z, k)d\sigma + (hw-|x|)\int_{0}^{|y|+hh} M(hw-|x|,\sigma, z, k)d\sigma\nonumber\\ &= -\frac{i}{2\pi k} \Big( (hh+|y|)\int_{|x|-hw}^{|x|+hw} M(hh+|y|,\sigma, z, k)d\sigma + (hh-|y|)\int_{|x|-hw}^{|x|+hw} M(hh-|y|,\sigma, z, k)d\sigma \nonumber\\ &\phantom{= -\frac{i}{2\pi k} \Big(} + (hw+|x|)\int_{|y|-hh}^{|y|+hh} M(hw+|x|,\sigma, z, k)d\sigma + (hw-|x|)\int_{|y|-hh}^{|y|+hh} M(hw-|x|,\sigma, z, k)d\sigma\Big), \end{eqnarray}

where $M(s,\sigma,z,k)$ is the kernel function

\[ M(s,\sigma,z,k) = \frac{exp(-ik\sqrt{\sigma^2+z^2+s^2}) - exp(-ikz)}{\sigma^2+s^2} \]

Parameters
sysparm
dataStructure holding element positions and f0
posPositions
nPositions# of positions
odatacomplex output
pBarprogress bar
Returns
error code

◆ CalcCwFocus()

int CalcCwFocus ( const sysparm_t< T > *  sysparm,
const ApertureData< T > &  data,
const T *  pos,
const size_t  nPositions,
std::complex< T > **  odata 
)

The positions must all equal the focus point and the number should match the number of elements. By doing so, a set of phases is computed for focusing. The function uses CalcHzFast for phase calculations.

Parameters
sysparm
data
pos
nPositions
odata
Returns

◆ CalcCwFocusNaiveFast()

int CalcCwFocusNaiveFast ( const sysparm_t< T > *  sysparm,
const ApertureData< T > &  data,
const T *  pos,
const size_t  nPositions,
std::complex< T > **  odata 
)

Compute CW response at multiple positions. The range of integration is naive so it is accurate when projections lie inside an element, but requires a huge amount of abcissas to get a usuable result, when projections lie outside an element.

Parameters
sysparm
data
pos
nPositions
odata
Returns

◆ CalcCwFocusRef()

int CalcCwFocusRef ( const sysparm_t< T > *  sysparm,
const ApertureData< T > &  data,
const T *  pos,
const size_t  nPositions,
std::complex< T > **  odata 
)

Reference implementation of the function above. Uses CalcCwFieldRef for phase calculations

Parameters
sysparm
data
pos
nPositions
odata
Returns

◆ CalcCwThreaded()

int CalcCwThreaded ( const fnm::sysparm_t< T > *  sysparm,
const ApertureData< T > *  data,
const T *  pos,
const size_t  nPositions,
std::complex< T > **  odata,
sps::ProgressBarInterface *  pbar 
)

Multi-threaded version of CalcCwFieldRef. This is the function to use.

Parameters
sysparm
data
pos
nPositions
odata
pbar
Returns

◆ CalcCwTimeReversal()

int CalcCwTimeReversal ( const fnm::sysparm_t< T > *  sysparm,
const ApertureData< T > *  pData0,
const ApertureData< T > *  pData1,
const T *  pos,
const size_t  nPositions,
const std::complex< T > *  pFieldValues,
const size_t  nComplexValues,
std::complex< T > **  odata,
sps::ProgressBarInterface *  pBar 
)

◆ CalcHz()

std::complex< T > CalcHz ( const T &  s,
const T &  l,
const T &  z,
const T &  k,
const GLQuad2D< T > *  gl 
)

Field above a corner of an element with dimensions $s$ and $l$ computed using Gauss-Legendre integration

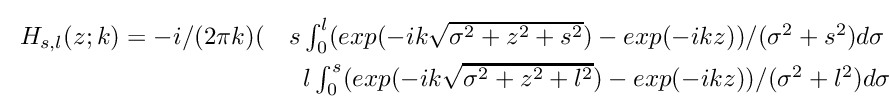
\begin{eqnarray*}H_{s,l}(z;k) = - i/(2\pi k) ( &s \int_0^l (exp(-ik\sqrt{\sigma^2+z^2+s^2}) - exp(-ikz)) / (\sigma^2+s^2) d\sigma + \\ &l \int_0^s (exp(-ik\sqrt{\sigma^2+z^2+l^2}) - exp(-ikz)) / (\sigma^2+l^2) d\sigma) \end{eqnarray*}

Reference implementation, see Rapid calculations of time-harmonic nearfield pressures produced by rectangular pistons, J. McGough, 2004

Parameters
swidth (x-dimension)
lheight (y-dimension)
zdistance to element
kwave-number
glAbcissae and weights for integration
Returns
Complex field value

◆ CalcSingleFast()

std::complex< T > CalcSingleFast ( const T &  s1,
const T &  s2,
const T &  l,
const T &  z,
const T &  k,
const T *  uxs,
const T *  uweights,
const size_t  nUs 
)

CalcSingleFast. TODO: Implement this for double

Parameters
s1lower limit
s2upper limit
ladjacent edge
zz-coordinate
kwave numer
uxsabcissae
uweightsweights
nUsnumber of abcissae
Returns
Complex field value
Generated on Tue May 17 2022 09:21:06 for SOFUS by doxygen 1.9.4